A Bidirectional, Holonomic RRT Path Planner
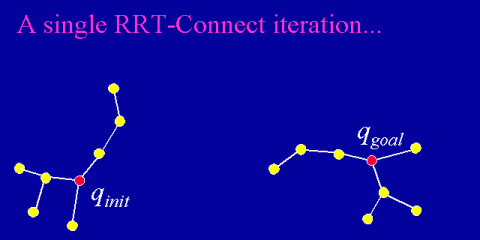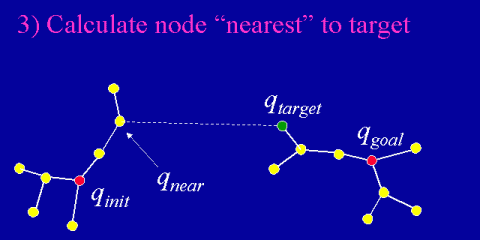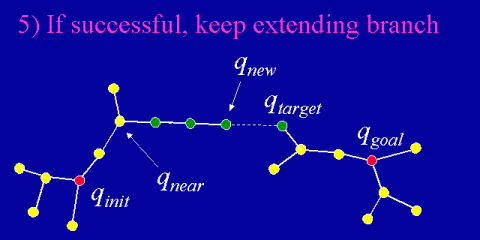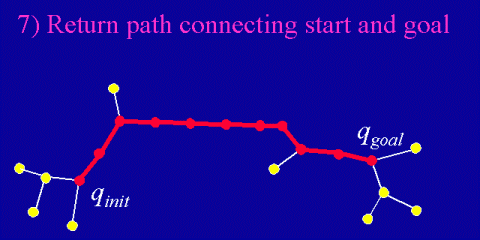
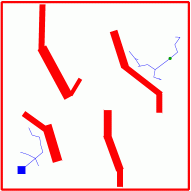
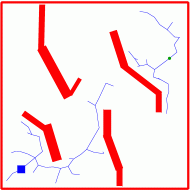
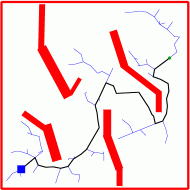
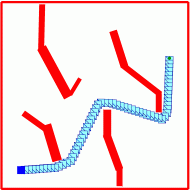
The fundamental operation used in growing an RRT is the EXTEND
operation depicted in the animation below. Given a target
configuration (randomly selected or not), a distance metric defined on
the configuration space is used to calculate the node q_near in
the existing tree that is nearest to a target configuration
q_target.
|
 |
 |
 |
 |
Here is a link to a collection of pictures and animations of a variety of example path planning problems.
Analysis
RRTs are biased to expand towards unexplored regions of the space, which is why they are called "rapidly-exploring". The greedy behavior in growing branches towards target configurations and attempting to connect the two trees allows many planning queries to be solved very efficiently. Despite this greediness, the limiting distribution of nodes in an RRT have been shown to ultimately converge towards the sampling distribution, even for non-convex spaces. (see references)
Like most heuristic search algorithms, RRT-Connect sacrifices path optimality and completeness in exchange for practical efficiency in searching high dimensional spaces. However, the paths computed have been observed to be relatively short, and rarely suffer from loops or self-intersections. In addition, the algorithm has been shown to be probabilistically complete, which means that the probability of failing to find a solution path (if one exists) decreases exponentially with planning time.
The main drawback to the algorithm is its frequent use of nearest-neighbor queries. A simple brute-force linear algorithm for computing nearest neighbors works fine for trees with approximately less than 20,000 - 40,000 nodes. For difficult planning queries requiring larger trees, efficient data structures and algorithms are needed to quickly locate nearest neighbors (e.g. BSPs, k-d trees).
References
- Download papers and further information.